目錄:
1. 介紹
2. 練習
1. 介紹
(I) 消除不必要的東西
這些東西可以是未知數(unknowns)、變數(Variables)等等不是答案的東西都是不必要,如果我們能把所有不必要的東西都用代入法消除掉後,剩下的就自然是我們想要的答案了。
例:2019 DSE/MC/Q3
求β: (x - 8)(x + α) - 6 = (x - 9)2 + β
因為我們只想要β,所以我們的目的就是要透過代入法消除x、α,但由於α是常數(Constant),所以我們不能把α代入成其他數值,但我們能Sub x = 8 去消除α,一次消除兩個不必要的東西
即會得出 -6 = 1 + β
(II) 簡化題目
許多時候DSE的題目都會出現一個未知常數(unknown constant),例如α,然後叫同學計算一個有α的答案,我們要做的,就是把α代入成一個數字去方便我們計算。
例:2019 DSE/MC/Q34
首先,我們先把題目改變成以下樣子
接著,我們設a = 0,那麼題目就會變成
而A、B、C、D的答案亦會分別變成 -1、1、-2、2,接著用計算機計出上述答案,若同學們不了解如何用計算機計算複數(Complex number),可參考站主的另一篇文章
計算後得出 2,那麼答案就是D。
有同學會問﹕「怎樣決定代入的數字呢﹖」,其實決定代入的數字主要取決於兩個條件﹕
(i) 答案不重複
我們決定代入的數字必須令到答案不重複,上述的例子代入a = 0後得出四個不重複的答案-1、1、-2、2。試想想,如果你代入一個數字後得出0、0、1、-1,而你計算題目後得出0,你能確定答案是A還是B嗎﹖當然不能﹗所以我們決定的數字首要條件就是令到四個答案都不重複,才能方便我們更快地尋找答案。
(ii) 方便性
除了「答案不重複」這個條件外,還有方便程度,同學們當然希望代入後能更快計算答案,而不是事倍功半,因此我們決定代入的數字時,還要考慮代入後的計算夠不夠簡單。我們再以剛剛的題目為例子﹕假設我們代入a = 0 or 0.5 or 3都會計出abcd四個不同的答案時,你會選擇把a代入那個數呢﹖當然是 0,相比起0.5、3,代入0代表的就是直接抹去a、也省卻了計算a2的步驟。 因此,在同學在持續練習代入法 (Substitution)後,會發現一個規律﹕我們代入的數不外乎, -1、0、1、0o、30o、60o、90o
2. 練習
更新中

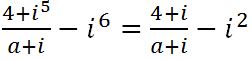







沒有留言:
張貼留言